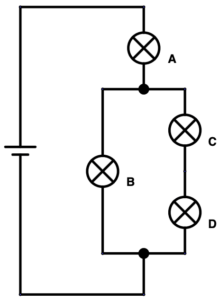
| raus- geschraubt | A | B | C | D |
|---|---|---|---|---|
| nichts | ☀︎ | ☀︎ | ☽ | ☽ |
| A | ✘ | ☼ | ☼ | ☼ |
| B | ☽ | ✘ | ☽ | ☽ |
| C | ☀︎ | ☀︎ | ✘ | ☼ |
| D | ☀︎ | ☀︎ | ☼ | ✘ |
| AB | ✘ | ✘ | ☼ | ☼ |
| AC | ✘ | ☼ | ✘ | ☼ |
| AD | ✘ | ☼ | ☼ | ✘ |
| BC | ☼ | ✘ | ✘ | ☼ |
| BD | ☼ | ✘ | ☼ | ✘ |
| CD | ☀︎ | ☀︎ | ✘ | ✘ |
☽ leuchtet schwach
☼ leuchtet nicht
✘ rausgeschraubt
- Es muss Lampe A eingeschraubt sein, damit etwas leuchtet.
- Ist Lampe B rausgeschraubt, leuchten die verbleibenden Lampen gleich hell.
- Lampen C und D leuchten schwach bis kaum erkennbar.
- Wird Lampe C oder D entfernt, leuchten Lampen A und B gleich hell. Die verbleibende Lampe leuchtet nicht.
Lampen C und D sind in Reihe geschalten. Dazu ist Lampe B parallel geschalten.
Zur Parallelschaltung der Lampen B, C und D ist Lampe A in Reihe geschalten.
Es handelt sich im eine gemischte Parallel- und Reihenschaltung. Lampe A leuchtet am hellsten, da über ihr die größte Spannung abfällt, da der Gesamtwiderstand der parallel geschalteten Lampen B und CD niedriger ist als der kleinste Einzelwiderstand.
Lampe B leuchtet heller als die Lampen C und D, da die Spannung, die an Lampe C anliegt, die gleiche ist, die an der Reihenschaltung der Lampen C und D anliegt.
Gegeben: U_0=7 V
R_{Lampe}=17,5 \Omega
Widerstand: Der Gesamtwiderstand muss schrittweise berechnet werden. Es werden zunächst Reihenschaltungen, dann Parallelschaltungen zusammengefasst. Dies muss hier wiederholt werden!
Die Lampen C und D haben einen Gesamtwiderstand von R_{CD} = 2 \cdot R_{Lampe} = 35 \Omega .
Die Lampen B sowie die beiden Lampen CD sind parallel zueinander geschalten. Ihr Gesamtwiderstand ist
\frac{1}{R_{BCD}} = \frac{1}{R_B} + \frac{1}{R_{CD}} = \frac{1}{17,5 \Omega } + \frac{1}{35 \Omega}
R_{BCD} = \frac{1}{\frac{1}{R_B} + \frac{1}{R_{CD}}} = 11,66 \Omega
Die Lampe A ist dazu in Reihe geschalten. Der Gesamtwiderstand ist also:
R_{Ges} = R_A + R_{BCD} = 17,5 \Omega + 11,66 \Omega = 29,16 \Omega
Spannung: Die Spannung teilt sich proportional zum Widerstand auf.
Im Spannungsteiler der Lampen A sowie BCD gilt: U_A = \frac{R_A}{R_{Ges}} \cdot U_0 = \frac{17,5 \Omega }{29,16 \Omega }\cdot 7V =4,2 V bzw. U_{BCD} = U_{B} = U_{CD} = \frac{R_{BCD}}{R_{Ges}} \cdot U_0 = \frac{11,66 \Omega }{29,16 \Omega} \cdot 7V = 2,79 V
Die Spannung U_{CD} = 2,79 V teilt sich gleichmäßig auf die Lampen C und D auf: U_C = U_D = \frac{1}{2} \cdot U_{CD} = 1,39 V .
Stromstärke: Die Gesamtstromstärke ist nach dem Ohmschen Gesetz
I = \frac{U_0}{R_{Ges}} = \frac{7V}{29,16 Ω}=0,24A . Diese Stromstärke fließt durch die Lampe A: I_A = I = 0,24A .
Diese Stromstärke teilt sich auf die Lampen B sowie CD auf. Die Teilstromstärken können ebenfalls mit dem Ohmschen Gesetz berechnet werden. Wir rechnen mit der im „unteren“ Teil anliegenden Spannung von U = 2,79 V :
I_B = \frac{U_{unten}}{R_B} = \frac{2,79 V}{17,5 \Omega } = 0,16 A bzw. I_{CD} = I_C = I_D = \frac{U_{unten}}{R_{CD}} = \frac{2,79 V}{35 \Omega } = 0,08 A .