• Es muss entweder Lampe A oder Lampe B eingeschraubt sein, damit etwas leuchtet.
• Ebenso: Es muss entweder Lampe C oder Lampe B eingeschraubt sein, damit etwas leuchtet.
• Wird Lampe A rausgeschraubt, leuchtet Lampe B deutlich heller (und andersrum).
• Wird Lampe C rausgeschraubt, leuchtet Lampe D deutlich heller (und andersrum).

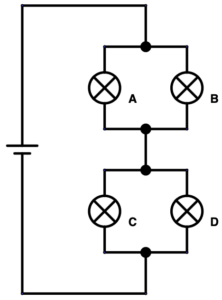
Die Lampen A und B sind parallel geschaltet. Ebenso sind Lampen C und D parallelgeschaltet. Beide Lampenpaare sind zueinander in Reihe geschalten.

Die Spannung beeinflusst, wie viel Energie von der Lampe gewandelt werden kann. In einer Reihenschaltung verteilt sich die Spannung proportional zum Widerstand. Der Gesamtwiderstand einer Parallelschaltung ist kleiner als der kleinste Widerstand in der Schaltung (hier: die Hälfte).

Drei eingeschraubte Lampen: Das bedeutet aber, dass an den beiden parallel geschalteten Lampen (kleiner Gesamtwiderstand) eine deutlich geringere Spannung abfällt als an der einzelnen Lampe. Dadurch leuchtet die einzelne Lampe deutlich heller.

Gegeben: U_0 = 7\,\mathrm{V}

R_{\mathrm{Lampe}} = 17{,}5\,\Omega

Widerstand:

Alle vier Lampen eingeschraubt: Die Gruppen A und B sowie C und D sind jeweils parallel geschaltet. Ihr Widerstand ist:

\frac{1}{R_{AB}} = \frac{1}{R_{CD}} = \frac{1}{R_{\mathrm{Lampe}}}+\frac{1}{R_{\mathrm{Lampe}}} = \frac{2}{R_{\mathrm{Lampe}}}

R_{AB} = R_{CD} = \frac{R_{\mathrm{Lampe}}}{2} = \frac{17{,}5\,\Omega}{2} = 8{,}75\,\Omega

Da die beiden Gruppen in Reihe geschaltet sind, ist der Gesamtwiderstand:

R_{\mathrm{ges}} = R_{AB}+R_{CD} = 17{,}5\,\Omega

Eine Lampe entfernt: Wird beispielsweise Lampe A entfernt, entfällt in dieser Gruppe die Parallelschaltung. Der Gesamtwiderstand ist dann:

R_{\mathrm{ges}} = R_B+R_{CD} = 17{,}5\,\Omega+8{,}75\,\Omega = 26{,}25\,\Omega

Spannung:

Alle vier Lampen eingeschraubt: Da die beiden parallelen Gruppen den gleichen Widerstand besitzen, fällt an jeder Gruppe die Hälfte der Gesamtspannung ab. Da die Lampen innerhalb einer Gruppe parallel geschaltet sind, liegt an jeder Lampe dieselbe Spannung an:

U_A = U_B = U_C = U_D = \frac{1}{2}\cdot U_0 = 3{,}5\,\mathrm{V}

Eine Lampe ausgeschraubt: Wird beispielsweise Lampe A entfernt, fällt über Lampe B eine Spannung von

U_B = \frac{R_B}{R_{\mathrm{ges}}}\cdot U_0 = \frac{17{,}5\,\Omega}{26{,}25\,\Omega}\cdot7\,\mathrm{V} = 4{,}67\,\mathrm{V}

ab. Über den parallel geschalteten Lampen C und D liegt dann jeweils

U_C = U_D = U_0-U_B = 2{,}33\,\mathrm{V}

Stromstärke:

Alle vier Lampen eingeschraubt: Durch jede Lampe fließt

I_{\mathrm{Lampe}} = \frac{3{,}5\,\mathrm{V}}{17{,}5\,\Omega} = 0{,}20\,\mathrm{A}

Der Gesamtstrom ist:

I_{\mathrm{ges}} = 2\cdot I_{\mathrm{Lampe}} = 0{,}40\,\mathrm{A}

Eine Lampe herausgeschraubt: Wird beispielsweise Lampe A entfernt, fließt durch Lampe B der Gesamtstrom:

I_B = \frac{U_B}{R_{\mathrm{Lampe}}} = \frac{4{,}67\,\mathrm{V}}{17{,}5\,\Omega} \approx 0{,}27\,\mathrm{A}

Dieser Strom teilt sich gleichmäßig auf C und D auf:

I_C = I_D = \frac{1}{2}I_B \approx 0{,}13\,\mathrm{A}